Metric TSP

In this example we execute Christophides algorithm which computes a 3/2-approximate tour in the metric TSP.

Start by importing the package.

import jgrapht
from jgrapht.algorithms.tour import metric_tsp_christofides

We create a complete graph where weights satisfy the triangle inequality.

g = jgrapht.create_graph(directed=False, weighted=True)

g.add_vertex(0)
g.add_vertex(1)
g.add_vertex(2)
g.add_vertex(3)
g.add_vertex(4)

g.add_edge(0, 1, weight=1)
g.add_edge(0, 2, weight=2)
g.add_edge(0, 3, weight=1)
g.add_edge(0, 4, weight=1)
g.add_edge(1, 2, weight=1)
g.add_edge(1, 3, weight=2)
g.add_edge(1, 4, weight=1)
g.add_edge(2, 3, weight=1)
g.add_edge(2, 4, weight=1)
g.add_edge(3, 4, weight=1)

print(g)

Out:

({0, 1, 2, 3, 4}, {0={0,1}, 1={0,2}, 2={0,3}, 3={0,4}, 4={1,2}, 5={1,3}, 6={1,4}, 7={2,3}, 8={2,4}, 9={3,4}})

Then, we execute Christophides algorithm.

tour = metric_tsp_christofides(g)

The result is an instance of GraphPath

tour_start = tour.start_vertex
tour_edges = tour.edges
tour_weight = tour.weight

print('Tour starts at: {}'.format(tour_start))
print('Tour edges: {}'.format(tour_edges))
print('Tour weight: {}'.format(tour_weight))

Out:

Tour starts at: 4
Tour edges: [8, 4, 0, 2, 9]
Tour weight: 5.0

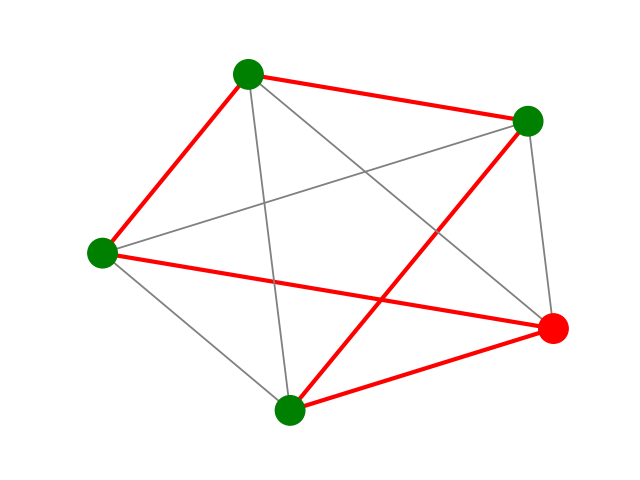
We next plot the graph and the tour.

import jgrapht.drawing.draw_matplotlib as drawing
import matplotlib.pyplot as plt

positions = drawing.layout(g, name="fruchterman_reingold", seed=17)
vertex_color = ['red' if v == tour_start else 'green' for v in g.vertices]

non_tour_edges = g.edges - tour_edges

drawing.draw_jgrapht_vertices(g, positions=positions, vertex_color=vertex_color)
drawing.draw_jgrapht_edges(g, positions=positions, edge_list=tour_edges, edge_linewidth=3, edge_color='red')
drawing.draw_jgrapht_edges(g, positions=positions, edge_list=non_tour_edges, edge_color='gray')

plt.show()