Minimum Spanning Tree using Prim

In this example we create an undirected graph and compute a minimum spanning tree (MST) using Prim’s algorithm. The graph is constructed using the Watts-Strogatz model.

Start by importing the package

import random
import jgrapht
import jgrapht.generators as gen
import jgrapht.algorithms.spanning as spanning
import jgrapht.drawing.draw_matplotlib as drawing
import matplotlib.pyplot as plt

Creating a graph is done using the factory method. We create an undirected graph with support for weights.

g = jgrapht.create_graph(directed=False, weighted=True)

We use the Watts-Strogatz generator to populate a graph. We start with the ring of 30 vertices each connected to its 4 nearest neighbors and rewiring with probability 0.1.

gen.watts_strogatz_graph(g, 10, 4, 0.2, seed=17)

We also assign some random weights from [0, 1) to the edges.

rng = random.Random(17)
for e in g.edges:
    g.set_edge_weight(e, rng.random())

Let us print the graph

print(g)

Out:

({0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, {0={0,1}, 1={0,2}, 2={1,2}, 3={1,3}, 4={2,3}, 5={2,4}, 6={3,4}, 8={4,5}, 9={4,6}, 10={5,6}, 11={5,7}, 12={6,7}, 13={6,8}, 14={7,8}, 15={7,9}, 16={8,9}, 17={8,0}, 18={9,0}, 19={9,1}, 20={3,0}})

Then, we execute Prim’s algorithm.

mst_weight, mst_edges = spanning.prim(g)

The result is a tuple which contains the weight and the minimum spanning tree.

print('mst weight: {}'.format(mst_weight))
print('mst tree: {}'.format(mst_edges))

Out:

mst weight: 2.686530568250198
mst tree: {0, 17, 19, 3, 5, 8, 9, 12, 14}

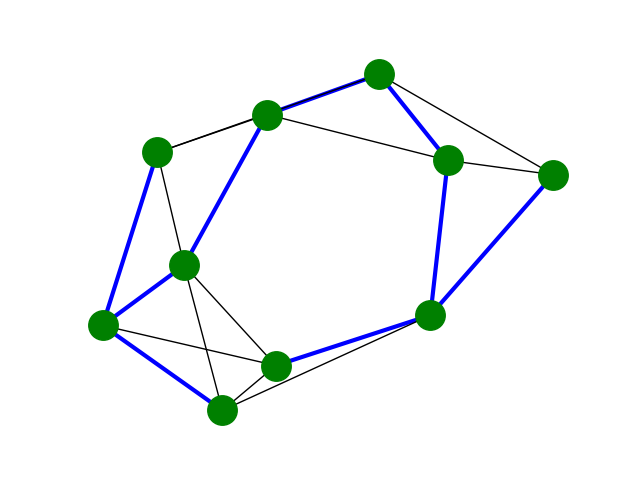
Ploting the graph with highlighted the MST edges

positions = drawing.layout(g, name="fruchterman_reingold", seed=17)

drawing.draw_jgrapht_vertices(g, positions=positions)

non_mst_edges = g.edges - mst_edges
drawing.draw_jgrapht_edges(g, positions=positions, edge_list=mst_edges,
    edge_color='blue', edge_linewidth=3)
drawing.draw_jgrapht_edges(g, positions=positions, edge_list=non_mst_edges,
    edge_linewidth=1)

plt.show()