Connected Components

In this example we demostrate how to find connected components in undirected graphs.

Start by importing the package.

import jgrapht
import jgrapht.algorithms.connectivity as cc
import jgrapht.drawing.draw_matplotlib as drawing
import matplotlib.pyplot as plt

We start by creating a graph with 4 connected components.

g = jgrapht.create_graph(directed=False, weighted=True)

for i in range(11):
    g.add_vertex(i)

g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 3)

g.add_edge(4, 5)
g.add_edge(5, 6)
g.add_edge(6, 7)

g.add_edge(8, 9)

print(g)

Out:

({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {0={0,1}, 1={1,2}, 2={2,3}, 3={4,5}, 4={5,6}, 5={6,7}, 6={8,9}})

Then, we execute the connected components algorithm.

is_connected, connected_components_it = cc.is_connected(g)
connected_components = list(connected_components_it)

The result is a tuple which contains whether the graph is connected and an iterator over the connected components.

print('is connected: {}'.format(is_connected))

for i, cc in enumerate(connected_components):
    print('Connected component {}: {}'.format(i, cc))

Out:

is connected: 0
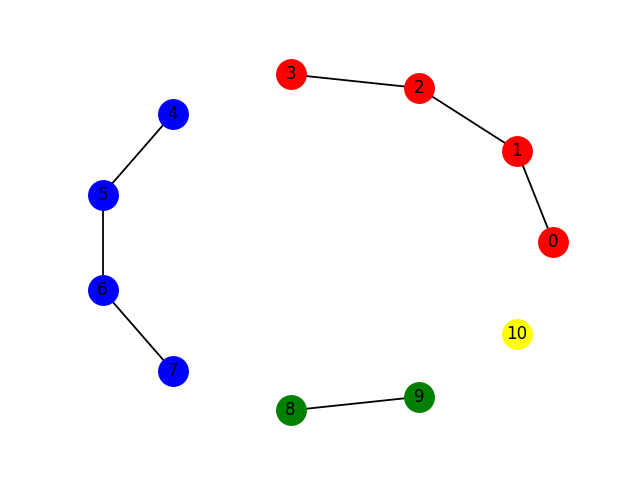
Connected component 0: {0, 1, 2, 3}
Connected component 1: {4, 5, 6, 7}
Connected component 2: {8, 9}
Connected component 3: {10}

Ploting the graph with a circular layout and separate color per connected component.

positions = drawing.layout(g, name="circular", seed=17)

vertex_labels = {v:str(v) for v in g.vertices}
colors = ['red', 'blue', 'green', 'yellow']
for cc, color in zip(connected_components, colors):
    drawing.draw_jgrapht_vertices(g, positions=positions, vertex_list=cc, vertex_color=color)

drawing.draw_jgrapht_vertex_labels(g, positions=positions, labels=vertex_labels)
drawing.draw_jgrapht_edges(g, positions=positions)

plt.show()