Coloring

In this example we color a graph using a greedy algorithm which uses saturation degree ordering. The saturation degree of a vertex is defined as the number of different colors to which it is adjacent. The algorithm always selects the vertex with the largest saturation degree.

Start by importing the package.

import jgrapht
from jgrapht.algorithms.coloring import greedy_dsatur

We create a graph which has 3 communities.

g = jgrapht.create_graph(directed=False)

for i in range(16):
    g.add_vertex(i)

g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(1, 3)
g.add_edge(1, 4)

g.add_edge(5, 6)
g.add_edge(6, 7)
g.add_edge(7, 8)
g.add_edge(8, 9)
g.add_edge(9, 10)
g.add_edge(5, 8)
g.add_edge(5, 10)

g.add_edge(11, 12)
g.add_edge(12, 13)
g.add_edge(13, 14)
g.add_edge(11, 15)
g.add_edge(12, 15)

g.add_edge(1, 5)
g.add_edge(9, 11)

print(g)

Out:

({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}, {0={0,1}, 1={1,2}, 2={2,3}, 3={3,4}, 4={1,3}, 5={1,4}, 6={5,6}, 7={6,7}, 8={7,8}, 9={8,9}, 10={9,10}, 11={5,8}, 12={5,10}, 13={11,12}, 14={12,13}, 15={13,14}, 16={11,15}, 17={12,15}, 18={1,5}, 19={9,11}})

Then, we execute the greedy coloring algorithm.

num_colors, color_map = greedy_dsatur(g)

print(num_colors)
print(color_map)

Out:

3
{0: 1, 1: 0, 2: 2, 3: 1, 4: 2, 5: 1, 6: 0, 7: 1, 8: 0, 9: 1, 10: 0, 11: 0, 12: 1, 13: 0, 14: 1, 15: 2}

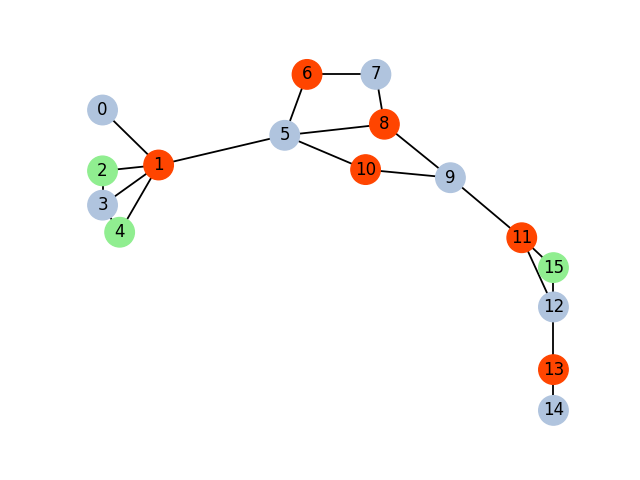
We next plot the graph with the colors.

int_to_actual_color = { 0: 'orangered', 1: 'lightsteelblue', 2: 'lightgreen' }
vertex_color = [ int_to_actual_color[color_map[v]] for v in g.vertices ]
vertex_labels = {v:str(v) for v in g.vertices}

import jgrapht.drawing.draw_matplotlib as drawing
import matplotlib.pyplot as plt

positions = drawing.layout(g, name="fruchterman_reingold", seed=17)

drawing.draw_jgrapht_vertices(g, positions=positions, vertex_color=vertex_color)
drawing.draw_jgrapht_vertex_labels(g, positions=positions, labels=vertex_labels)
drawing.draw_jgrapht_edges(g, positions=positions)

plt.show()